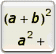Préparation 2

Dans une salle de jeu un appareil comporte 4 roues, chacune portant à sa périphérie 8 images de fruits différents:
                   Ananas, Bananes, Cerises, Dattes, Fraises, Groseilles, Poires, Raisins.

Une mise de 1€ déclenche le fonctionnement de l'appareil pour une partie.
Chacune des quatre roues affiche au hasard dans une fenêtre un de ces 8 fruits.

Exemple d'affichage :
            

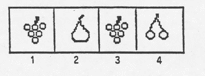
On admettra que tous les événements élémentaires sont équiprobables.

Calculez la probabilité des événements suivants :
E : on obtient quatre fruits identiques;
F : on obtient trois fruits identiques et trois seulement;
G : on obtient quatre fruits distincts.
Certains résultats permettent de gagner de l'argent :
50 euros pour quatre fruits identiques; 5 euros pour trois fruits identiques; 1 euro pour quatre fruits distincts;
0 euro pour les autres résultats.
Soit X la variable aléatoire qui à chaque résultat associe le gain indiqué ci-dessus (ne pas tenir compte de la mise).

a) Quelle est la probabilité de l'événement "obtenir un gain non nul "?
b) Déterminez l'espérance mathématique de X.
c) Calculer l'écart-type.

Solution