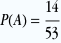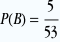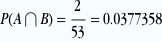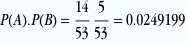Deux événements A et B sont indépendants ssi P(A∩B)=P(A) . P(B).
Autrement dit, deux événements sont indépendants s’ils ne peuvent se réaliser en même temps.
exemple: On tire une carte au hasard d’un jeu de 52 cartes. Les événements A=”obtenir un coeur ♥️️” et B=”obtenir un as️” sont-ils indépendants? A votre avis...?
Calculons la probabilité des deux événements.
puisqu’il y a 13 coeurs dans le jeu de 52 cartes;
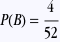puisqu’il y a 4 as dans le jeu de 52 cartes.Calculons maintenant la probabilité de l’intersection. A∩B est l’événement “obtenir un coeur et obtenir un as”, autrement dit “obtenir l’as de coeur”. Il n’y a qu’un seul as de coeur dans le jeu donc
Pour vérifier si les événements sont indépendants, vérifions la définition:
P(A∩B)=P(A) . P(B)
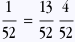
Donc oui, ils sont bien indépendants!
Pour comprendre de manière intuitive, posez-vous la question “je tire une carte; si on me dit que j’ai tiré un coeur, est-ce que du coup j’ai plus de chances (ou moins) d’avoir tiré un as ?” Non car il y a un as de coeur sur 13 coeurs (1/13), ce qui est la même proportion que d’as dans le jeu complet (4/52).
De même, si l’on me dit que j’ai tiré un as, ai-je plus de chances (ou moins) d’avoir tiré un coeur ? Non car il y a autant d’as de coeur que de pique, carreau ou trèfle.
En traduisant en formule, on peut aussi dire que P(A|B)=P(A) et P(B|A)=P(B)
Et si, en essayant de tricher, on ajoutait un deuxième as de coeur au jeu... ?*
