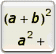|
Asymptote oblique
Exemple: 
dom f= 
 et 
il n'y a donc pas d'AH.
On remarque que, quand x→+∞, l'expression  → 0
et donc la fonction se rapproche de la droite y=x+2, l’écart entre les deux tendant vers 0.
On dit alors que la fonction f admet une asymptote oblique à droite d’équation y=x+2
|
Faites varier la valeur de l'abscisse a à l'aide du curseur. L'écart entre la fonction et la droite diminue quand a augmente.
Créé avec GeoGebra
|
De manière générale si  , alors f admet une asymptote oblique à droite d’équation y=a x + b.
Une fonction f admet une asymptote oblique AO ≡y=a x + b
SSI
 ∈ R
et
 ∈ R
remarque:
- Il faut donc que les deux limites  et  soient réelles. Sinon, il n’y a pas d’asymptote oblique à droite.
- Si a=0, l’asymptote est en fait une asymptote horizontale AH≡ y= b.
De la même manière, on parle d’asymptote oblique à gauche:
Une fonction f admet une asymptote oblique AO ≡y=a x + b
SSI
  ∈ R
et
 ∈ R
remarque:
- Si f admet une asymptote horizontale à droite, alors il n’y a pas d’asymptote oblique à droite. (Et de même à gauche)
Exercices
|
