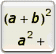| Introduction à la notion de dérivée

P est un point quelconque de la fonction f
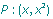
On considère la sécante à la fonction f passant par les points P et A:(1,1)
Déplacez le point bleu indiquant x, l'abscisse du point P vers 1, l'abscisse du point A
On constate que la position de la sécante tend à se rapprocher de la position de la tangente ( dessinée en rouge).
Calculons le coefficient angulaire de la sécante:
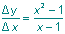
On obtient le coefficient de la tangente à la fonction au point A en calculant la limite
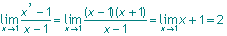
On peut appliquer le même procédé en prenant un autre point A sur la fonction
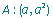
La pente de la tangente à la fonction au point A est donnée par la limite

Si cette limite existe, elle est appelée nombre dérivé de la fonction f en a et notée f'(a)
On peut alors considérer la fonction réelle qui à x fait correspondre le nombre dérivé de la fonction en x, c'est-à-dire f'(x).
On a alors: f'(x) = 2 x
Cette fonction est la fonction dérivée de la fonction f
|